Trust region
Trust region is a general strategy of optimization of an objective function by constructing an approximation of the function around a certain point and measuring its values at the nearest regions so as to select the correct direction for parameters change. While in line search strategy the optimal step size is selected based on the specified direction, in trust region the step size is defined by the maximum size of the trust region and only then the direction is determined.
The approximation at trust region with size $p$ is constructed using second-order Taylor expansion:
$\phi(p_k) = f_k + p_k^T \nabla f_k + \frac{1}{2} p_k^T B_k p_k$
where $x_k$ is the center of the trust region, $\nabla f_k$ is the gradient and point $x_k$, and $B$ is the Hessian or some approximation of it. Also $p_k$ is selected to be less of equal to some maximim radius value of the trust region $\Delta_k$.
The size of the trust region is critical for the effectiveness of the whole algorithm, as smaller regions, albeit more precise, increase the number of iterations. If the approximation is good enough for finding the minimum of the true function the trust region may be increased, otherwise it is reduced in order to select more precise direction.
We can validate the fitness of approximation by comparing the actual reduction of the function and the predicted one:
$\rho_k = \frac{f_k-f(x_k+p_k)}{\phi(0)-\phi(p_k)}$
Here $\phi(0)$ would be equal to $f_k$ which makes sense as the value of approximation is the same as the value of the true function at the centering point.
If $\rho_k$ is not positive then the radius of the trust region should be reduced. If $\rho_k$ is close to 1 then the model approximates the function very well, and the trust region may be expanded.
For quadratic function (and the approximation above is quadratic) under condition that Hessian is positive definite the minimum value within the trust region can be found with the Newton step like this:
$p_k^b = -B_k^{-1}\nabla f_k$
Also the newly detected point should not be outside the radius of the trust region.
$\lvert -B_k^{-1}\nabla f_k\rvert \leq \Delta_k$
These conditions do not always hold so an approximate solution should be found within the trust region. Below are descriptions of some of the trust region algorithms.
Cauchy point
Cauchy point is a solution to the problem of finding the minimum of a trust region which is determined along the direction of the steepest descent. At the center of the trust region just like in line search the gradient in measured is order to determine the direction of the steepest descent. Following this, the vector from the center to the edge of the trust region can be expressed like this:
$p_k^s = \Delta_k \frac{-\nabla f_k}{\left|\left|\nabla f_k\right|\right|}$
where $\Delta_k$ is the radius at $k$-th iteration.
The point of the minimum is searched for along this vector, so that it can be somewhere within the trust region.
$p_k^C = \tau_k p_k^s$,
$0 < \tau_k \leq 1$
Now the task is to find such $\tau_k$ where the quadratic approximation $\phi(\tau_k p_k^s)$ is at its minimum within the trust region.
$\phi(\tau p_k^s) = f_k + \nabla f_k^T \tau p_k^s + \frac{1}{2} \tau (p_k^s)^T B_k \tau p_k^s$
Taking the derivative with respect to $\tau$ and evaluating it at 0 we get:
$ \nabla f_k^T p_k^s + \tau (p_k^s)^T B_k p_k^s = 0$
From here
$\tau_k = \frac{-\nabla f_k^T p_k^s}{(p_k^s)^T B_k p_k^s}$
By substituting $p_k^s$ with the expression from above we have
$\tau_k = \frac{-\nabla f_k^T \Delta_k \frac{-\nabla f_k}{\left|\left|\nabla f_k\right|\right|}}{\Delta_k \frac{-\nabla f_k^T}{\left|\left|\nabla f_k\right|\right|} B_k \Delta_k \frac{-\nabla f_k}{\left|\left|\nabla f_k\right|\right|}} = \frac{ \left|\left|\nabla f_k\right|\right|}{\Delta_k \frac{\nabla f_k^T}{\left|\left|\nabla f_k\right|\right|^2} B_k \nabla f_k} = \frac{ \left|\left|\nabla f_k\right|\right|^3}{\Delta_k \nabla f_k^T B_k \nabla f_k}$
After solving this we may end up with $\tau_k$ greater than the radius of the trust region. In this case our step will be restricted to the border of the rust region along the direction of the steepest descent. Also, if $B_k$ is not positive definite then $\tau_k$ is taken to be equal to 1 as well. Below is an illustration of optimization via Cauchy point search.
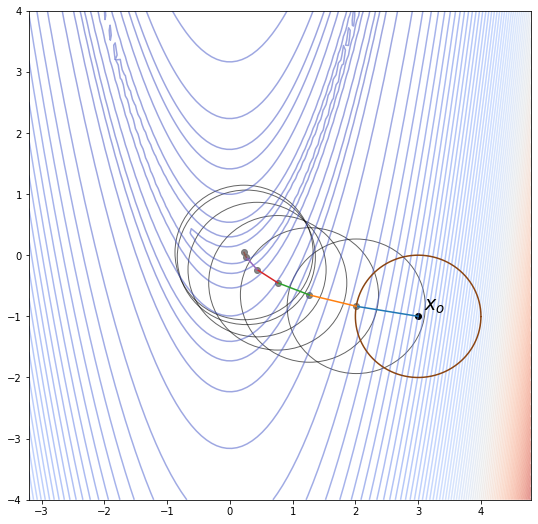
The contour plot shows the loss function which is dependent on two variables and the circles are trust regions on different iterations.
In fact, Cauchy point optimization can be viewed as the steepest descent with line search where the maximum step size is restricted with the radius of the trust region.
Dogleg method
This method can be applied if the Hessian of the function approximation is positive definite. According to this method if it is possible to make a Newton step within a trust region then such step is performed. If the Newton step finds a minimum outside the borders of the trust region then the algorithm selects a point on the border which intersects the line connecting Cauchy point and the point obtained with the Newton step.
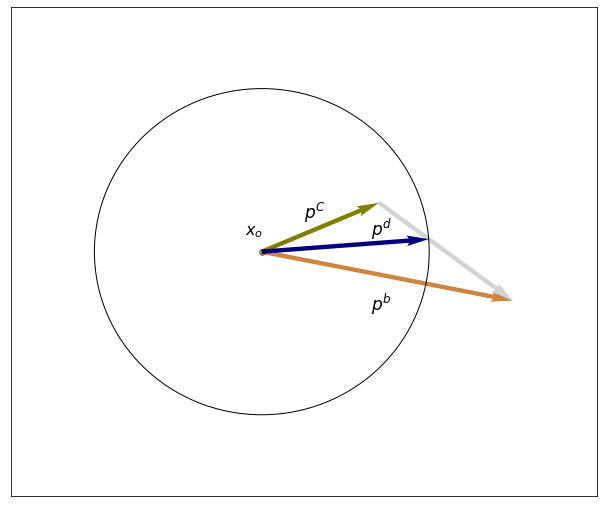
On the image above the vector displaying the dogleg step is marked as $p^d$. Essentially $p^d$ is a sum of $p^C$ and a fraction of another vector pointing from the Cauchy point to the point determined by Newton step ($p^b - p^C$). Let’s indicate this fraction as $\beta$. From here were have an equation which compares the lengths of the radius and the step $p^d$.
$\lvert\lvert p^C + \beta(p^b - p^C) \rvert\rvert^2 = \Delta_k^2$
The equation is solved analytically for $\beta$, so that the new point can be selected as $x_k + \beta(p_k^b - p_k^C)$