Nedler-Mead algorithm

The Nedlear-Mead optimization algorithm employs the concept of simplex - a special type of polytope in $n$-dimensional space which has $n+1$ vertices, that is the points where lines meet. For example, in 2-dimensional space a simplex will assume the form a triangle, and in 3-dimensional space it will become a tetrahedron.

According to the algorithm, dimensions represent variables of a function which has to be optimized. By taking $n+1$ guesses of parameters we obtain points in an $n$-dimensional space, which can be viewed as the vertices of a simplex. The best set of parameters is found by iterative reduction (and stretching) of the space which is spanned by the vertices of the simplex. Below is an example of how the space might be reduced during several iterations if we have two variables and a function which has to be minimized.

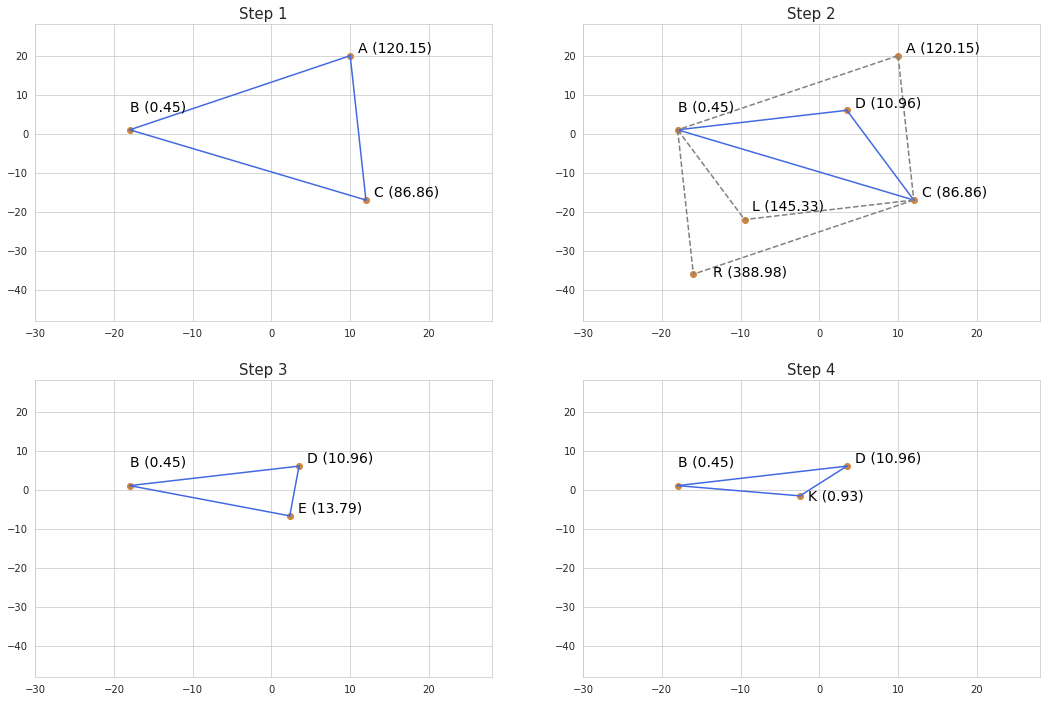
Points $A$, $B$ and $C$ are the initial set of guesses. The function is evaluated for each guess - on the chart we see its values in the parentheses. The algorithm starts off by selecting a point of the worst guess (in our case point $A$) and shifting it towards the opposite side of the simplex. At first its reflection over the line $BC$ at point $R$ is evaluated. In our case the new point is not better than the old one so we contract the simplex by moving both points $A$ and $R$ towards $BC$ by half of the distance, and evaluate the function at them as well. We observe that at point $D$ the function has smaller value than at point $L$ so we select it as the replacement of the original point $A$. If we had reached the best value at point $R$ we would have decided to stretch the simplex further in that direction by moving point $R$ even farther away from $BC$ - perhaps the function would have produced even smaller values in that area. In addition, if neither $L$ nor $D$ would produce the desired improvement we could also contract the simplex by shifting all points towards the point of the best available fit.

In the next iteration the simplex is further reduced by moving point $C$ towards its center and producing a new point $E$. The algorithm goes on until some stopping criterion is reached.