Text similarity
Doing text analysis you may encounter a case when you need to select the most similar text or a group of text to another chosen text.
One way to do it is to calculate Levenshtein distance between texts. This metric basically represents the number of single-character transformations such as word insertion, removals or substitution needed for one text to become another one. For example, the word “swan” is two points away from the word “swamp” as it needs to have one character substituted and another one added, while “Levenshtein” and “Levenstein” are only 1 point away (guess why).
Although calculating Levenshtein distance might be a good technique for detecting small phrases with typos and matching them to the real ones it is not efficient for comparing longer texts with similar context but another word order. Swapping and adding complete words might cost too many points of Levenshtein distance while proving the text to be dissimilar when in fact they bear the same context.
Another option to find similar texts is to produce n-dimensional vectors of word counts for each of the texts, where n is the number of unique words in all texts. By doing so we are placing each text within space of orthogonal vectors. Then these vectors can be compared in terms of their “closeness” with regard to the angle between them.
Let’s recall that cosine of an angle between two vectors can be computed with the dot product:
$\cos{\alpha} = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{\lVert a\rVert \cdot \lVert b\rVert }$
Now imagine a simplified example where we have three texts with words belonging to three categories: business, infrastructure and people. Here is the word count for each category within each text:
| business | infrastructure | people | |
|---|---|---|---|
| Text A | 3 | 5 | 10 |
| Text B | 4 | 7 | 20 |
| Text C | 10 | 6 | 2 |
And here is the vector representation in three-dimensional space:
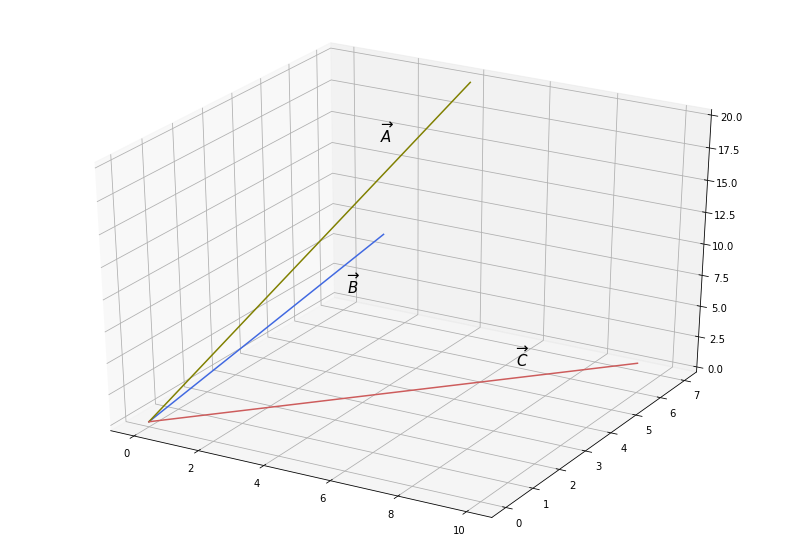
As we can see, vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ seem to be closer to each other than to $\overrightarrow{C}$.
Certainly, this example is way too simple, and in a real-world scenario depending on the situation there might be a necessity to remove common words, known as stop-words, which bear no additional context. In addition, some word categorizing might be applied before producing vectors in order to reduce the number of dimensions and group words from the same or similar context.
Furthermore, for those pairs of vectors which have similar angle between them additional comparison based on Euclidean distance may be conducted. In fact, it will simply compare vector lengths, which will help to determine if there are texts which may be viewed as subsets of other texts.