Jensen’s Inequality
The Statement of the Inequality
In mathematics, Jensen’s Inequality is a fundamental and widely-used result that makes use of the properties of convex functions. It states that for a convex function $f$, and a random variable $X$, the following is true:
\[E[f(X)] >= f(E[X])\]Here, $E[X]$ is the expected value or mean of the random variable $X$.
In plain English, the inequality tells us that the expected value of a function of a random variable is always greater than or equal to the function evaluated at the expected value.
This inequality is a cornerstone for the algorithm called Expectation Maximization.
Understanding Convex Functions
To grasp Jensen’s Inequality, one must first understand the concept of a convex function. A function $f(x)$ is convex if a line segment connecting any two points on its graph lies on or above the graph itself. This creates a characteristic “smile” or bowl-like shape.
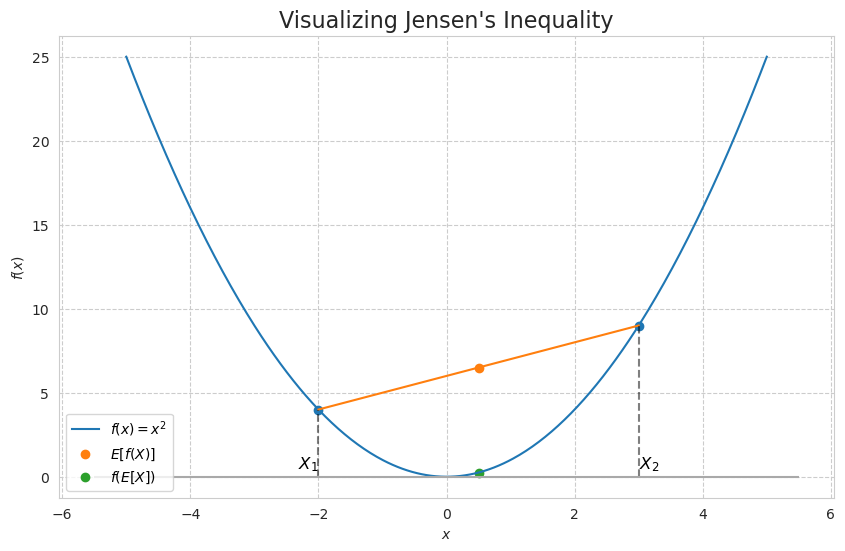
Mathematically, a function $f$ is convex if for any two points $x_1$ and $x_2$ in its domain and any value $\alpha$ between 0 and 1, the following holds:
\[f(\alpha x_1+(1−\alpha)x_2) \leq \alpha f(x_1)+(1−\alpha)f(x_2)\]A few common examples of convex functions include $f(x)=x^2$, $f(x)=∣x∣$, and $f(x)=e^x$.
Conversely, a concave function has an “upside-down smile” shape. For a concave function, the Jensen’s inequality is reversed.
Intuitive Example
Consider the convex function $f(x)=x^2$. Let’s take two numbers, x1=2 and x2=4.
The average of the function: First, we apply the function to each number and then take the average:
\[\frac{f(2)+f(4)}{2}=\frac{4+16}{2}=10\]The function of the average: First, we take the average of the numbers and then apply the function:
\[f(\frac{2+4}{2})=f(3)=3^2=9\]As the inequality predicts, $10 \geq 9$.