QR decomposition

QR decomposition may be a numerically stable algorithm for solving systems of linear equations. Similar to singular value decomposition it provides mechanism for efficient matrix decomposition into a set of new matrices which are easy to handle. In case of QR, the original matrix $A$ of size $n \times m$ is being decomposed into an orthonormal $n \times n$ matrix $Q$ and an upper-triangular $n \times m$ matrix $R$.

The upper-triangular matrix $R$ has the same rank as $A^{T}A$, and can be easily applied for for solving reduced system of linear equations with back substitution.

One drawback of using Householder decomposition is that the process is not parallelizable, as every reflection that produces zeros in the columns of $A$ matrix depends on the previous step.

Householder decomposition

Unlike traditional Gram-Schmidt QR decomposition, which may introduce instability in floating point numbers, Householder decomposition does not form matrix $Q$ explicitly but instead performs series of multiplications to the original matrix $A$ where each multiplication transforms one column of $A$ forming zeros in it.

\[A = \left[\begin{array}{ccccc} x & x & x & x & x \\ x & x & x & x & x \\ x & x & x & x & x \\ x & x & x & x & x \\ x & x & x & x & x \\ x & x & x & x & x \end{array} \right] , Q_1 A = \left[\begin{array}{ccccc} x & x & x & x & x \\ 0 & x & x & x & x \\ 0 & x & x & x & x \\ 0 & x & x & x & x \\ 0 & x & x & x & x \\ 0 & x & x & x & x \end{array} \right] , Q_2 Q_1 A = \left[\begin{array}{ccccc} x & x & x & x & x \\ 0 & x & x & x & x \\ 0 & 0 & x & x & x \\ 0 & 0 & x & x & x \\ 0 & 0 & x & x & x \\ 0 & 0 & x & x & x \end{array} \right]\]

The process is repeated until $A$ is fully transfromed into upper-triangular $R$.

So how do we get such $Q$ which transfrom a column of a matrix?
Let’s consider each column of $A$ as a vector. Since $Q$ is orthogonal, multilication of $A$ by $Q$ will not change the magnitude of each individual vector:

     $\left|\left|Q_n a\right|\right|_2 = \left|\left|a\right|\right|_2$

This means that the magnitude of a new vector will be the same as that of the original one. Considering that the transformed vector contains zeros after the first element it is fair to conclude that the transformed vector can be expressed by multiplication of the magnitude of the original vector and the unitary vector whose first element is 1 and the rest are zeros.

     $Qa = \left|\left|a\right|\right|_2 e_1 = \overrightarrow r$

Transforming a vector into a new one with the same magnitude but different direction can be viewed as reflection operation:

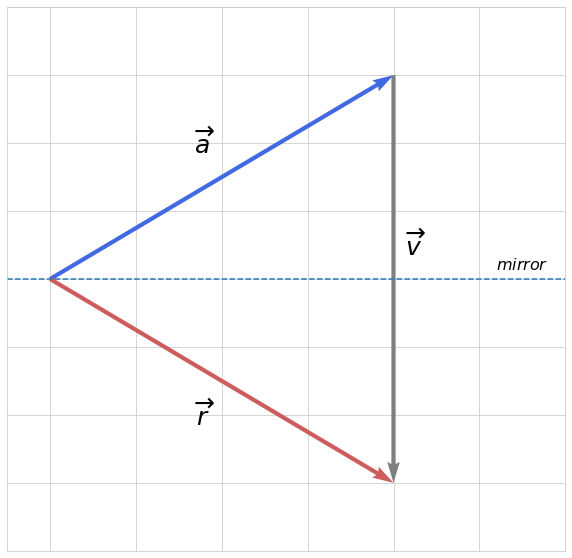
Here a vector $\overrightarrow a$ which corresponds to a column of original matrix $A$ is being reflected through “mirror” into vector $\overrightarrow r$ which represents a new transformed column with zeros after the first element (provided that this is the first operation in Householder transformation). We can also see that $\overrightarrow r$ is obtained by $\overrightarrow a$ + $\overrightarrow v$.

Let’s note that $\overrightarrow v$ is perpendicular to the “mirror”, thus $\overrightarrow v/2$ can be viewed as a projection of $-\overrightarrow a$ onto the space of $\overrightarrow v$.
The magnitude of such projection is a dot product of $-\overrightarrow a$ and the normalized version of $\overrightarrow v$ (see the related article):

     $ \left|\left|\overrightarrow v/2\right|\right|_2 = -a \frac{v}{||v||}$

And the vector of projection is simply the product of its magnitude and direction (the direction is the normalized version of $\overrightarrow v$):

     $\overrightarrow v/2 = -a \frac{v}{||v||} \cdot \frac{v}{||v||} = \frac{-a^{T}v}{\sqrt{v^{T}v}} \cdot \frac{v}{\sqrt{v^{T}v}} = v\frac{-a^{T}v}{v^{T}v}$

From here:

     $\overrightarrow v = 2v\frac{-a^{T}v}{v^{T}v}$

Now with regard to Householder decomposition, where $\overrightarrow r$ is obtained as $Qa$, the expression $\overrightarrow r = \overrightarrow a$ + $\overrightarrow v$ can be rewritten as follows:

     $Qa = a + 2v\frac{-a^{T}v}{v^{T}v}$, which boils down to this:

     $Q = I - \frac{2vv^{T}}{v^{T}v}$, where $v$ can be obtained as

     $v = r - a = \left|\left|a\right|\right|_2 e_1 - a$

The process is repeated for the next columns of $A$ until it becomes upper-triangular.

Since we do not want to transform already transformed columns of $A$, the matrix $Q$ of each next step is calculated for a smaller rank, which is obtained by removing upper row and left column from the $Q$ of previous step. However, in order to make possible multiplication with the previously transformed $A$ the matrix is expanded to the upper left again by adding 1 at the diagonal, or in general:

\[Q_k = \left[\begin{array}{cc} I_{k-1} & 0\\ 0 & Q_k \end{array} \right]\]