Mean value theorem

The mean value theorem states that if a function is continuous and differentiable between two points then there exists a point between them where the tangent line is parallel to the secant line crossing these two points. Here is an illustration:

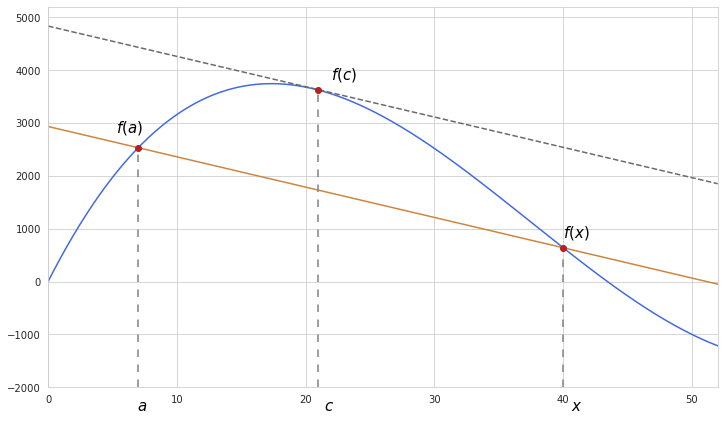
Here the secant line which crosses the function at $a$ and $b$ is parallel to the tangent line at point $c$ which is between $a$ and $b$. This is how the slope can be expressed:

     $f’ (c)=\frac{f(x)-f(a)}{x-a}$

It should be noted that the mean value theorem tells only about the existence of this point, not its value.

With help of this theorem the difference between the values of a function at different points can be expressed as a scaled version of the difference between the dependent variable values which depends on the slope that happens somewhere between these points.

     $f(x)-f(a) = f’ (c) \cdot (x-a)$

     $f(x) = f(a) + f’ (c) \cdot (x-a)$

The last equation is very similar to the first-order Taylor approximation where instead of $f’ (c)$ we would have $f’ (a)$. While using $f’ (c)$ produces the exact equation, a good approximation can be obtained with $f’ (a)$ instead, provided that the difference between $x$ and $a$ is reasonably small.

One way to express the mean value theorem is by viewing $x$ as a sum of $a$ and some delta (lets name in $p$). Then:

     $f(a+p) = f(a) + \nabla (a+tp)^T p$

where $t$ is a number between 0 and 1.

If the function is twice differentiable then we have:

     $\nabla (a+p) = \nabla f(a) + \int_0^1 \nabla^2 (a+tp) p dt$

So that the original function can be further decomposed using the second derivative:

     $f(a+p) = f(a) + f(a)^T p + \frac{1}{2} \nabla^2 p^T f(a+tp) p$

What we have obtained is very similar to the second-order Taylor approximation.