Limits and continuity

Let’s build an idea about formal definition of limit.

     $\displaystyle{\lim_{x \to c}f(x)}= L$

We can get $f(x)$ infinitely close to $L$ if we get values of $x$ sufficiently close to $c$. The limit only describes the behavior of a function as it approaches a point. It does not however tell us the value at that exact point.

Let’s suppose we have a function $f(x)=\frac{1}{\lvert x \rvert}$. By its graph we can see that when $x$ variable increases, the $y$ value goes to 0 but without quite reaching it.

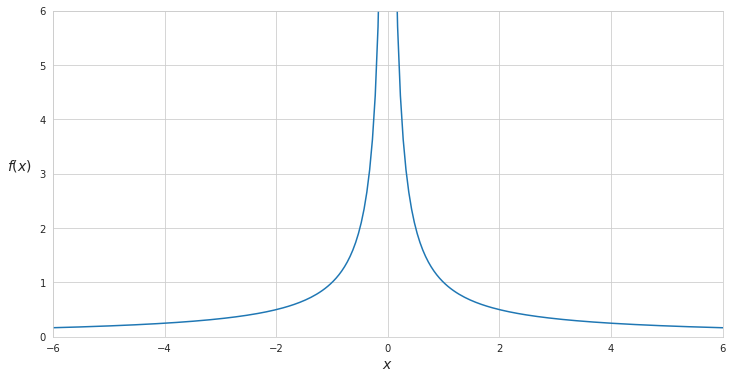
In fact, when we divide 1 by any positive number we might be getting infinitely small numbers but never 0. This is where the concept of limit arises. In our case the limit is 0 when $x$ goes to infinity: $\displaystyle{\lim_{x \to \infty}}=0$.
In the example above other limits can be seen when $x$ goes to 0: $\displaystyle{\lim_{x \to 0}}=\infty$, and when $x$ goes to minus infinity: $\displaystyle{\lim_{x \to -\infty}}=0$. In all cases the limits are unbounded.
We also see that the function is the example is discontinuous at the point where $x$ equls 0.

Under the formal definition of continuity $f(x)$ is continuous at $x=c$ if and only if the limit $\displaystyle{\lim_{x \to c}f(x)}$ equals $f(c)$. So to speak, continuity is present only when the function exists at the given point. On the other hand, discontinuity is observed when a function is interrupted at a certain point. There are three types of discontinuity:

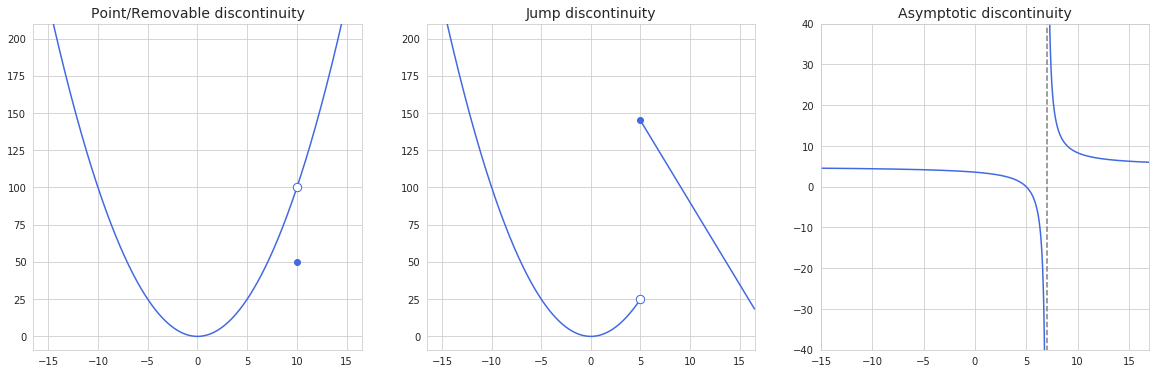
• Under the condition of point discontinuity two-sided limit exists. It can be seen from the graph that the limit $\displaystyle{\lim_{x \to 10}}$ exists from both sides and equals 100. However the value of the function at the point when $x$ equals 10 is 50. Therefore, with regard to the limit definition of continuity the function is discontinuous.
  
• When we have jump discontinuity, two one-sided limits exist, but they do not evaluate to the same value, so there is no two-sided limit to the function.
  
• Under the condition of asymptotic discontinuity both left- and right-handed limits are unbounded, so they don’t even exist and thus do not meet the requirement of continuity.