Fourier series
A Fourier series is a way to approximate a periodic function as the sum of simple sine and cosine functions which makes it useful for analyzing and synthesizing functions with periodic behavior, such as signals in signal processing or periodic phenomena in physics. The benefit of trigonometric functions is that they can be easily modeled and their derivatives are understood. Additionally, Fourier Series makes use of the orthogonality relationships of the sine and cosine functions.
Periodic function
A function is said to be periodic of period $P$ if $f(x+P) = f(x)$ for all $x$ in the domain of $f$. The smallest positive value of $P$ is called the fundamental period.
From the article on the complex numbers it can be seen that the relationship between $\sin (x)$ and $\cos (x)$ looks like a circle if $x$ assumes values from 0 to $2\pi$. If $x$ goes beyond $2\pi$ then the pattern simply repeats itself. The trigonometric functions $\sin x$ and $\cos x$ are the prime examples of periodic functions with fundamental period of $2 \pi$.
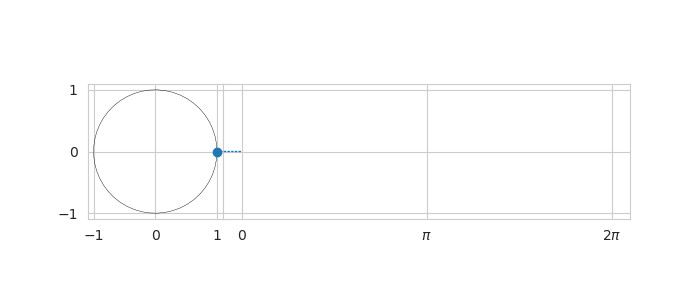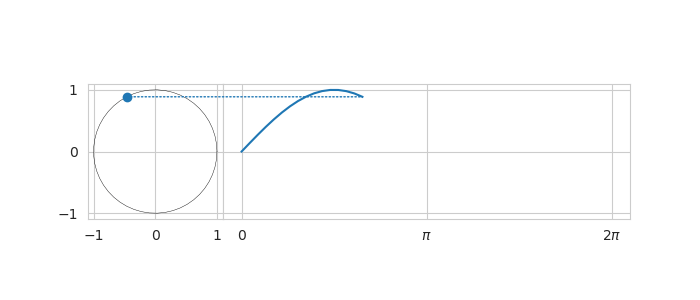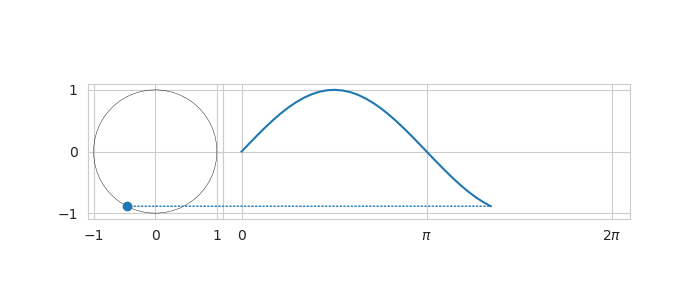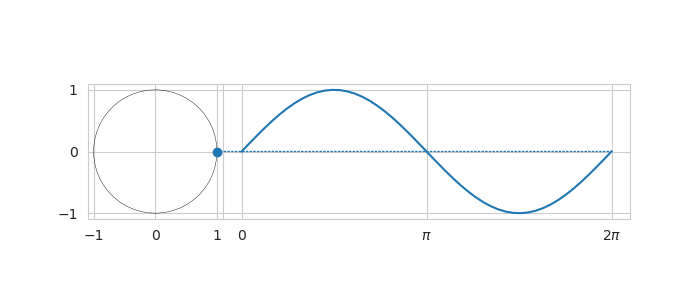
Fourier series formula
The general form of a Fourier series for a periodic function $f(t)$ with the period $P$ is given by:
\[f(t)=a_0 + \sum_{n=1}^{\infty} \left[ a_{n} \cos\left(\frac{2 \pi}{P}nt\right)+b_{n} \sin\left(\frac{2 \pi}{P}nt \right)\right]\]where:
- $a_0$ is the average value of the function over one period of $f(t)$
- $n$ is the harmonic number (harmonic frequency), indicating the frequency of the sine and cosine functions in the series. Higher values of $n$ correspond to higher frequencies.
- $a_n$ and $b_n$ are the Fourier coefficients, representing the amplitude of the $n$th cosine and sine components.
It should be noted that $P$ could just be equal to the whole period which we want to approximate using Fourier series.
Inclusion of the term $\frac{2\pi}{P}$ is the scaling of sine and cosine fundamental period $2 \pi$ with respect to the period of the function which is approximated.
The Fourier series essentially breaks down a complex periodic function into simpler sinusoidal components, each associated with a specific frequency. By including more terms in the series, it is posible approximate the original function more accurately. This is somewhat similar to what Taylor expansion does.
Below you can see a demo of Fourier series approximation of a step function. When the number of terms goes to infinity it is possible to approximate even functions with discontinuity.
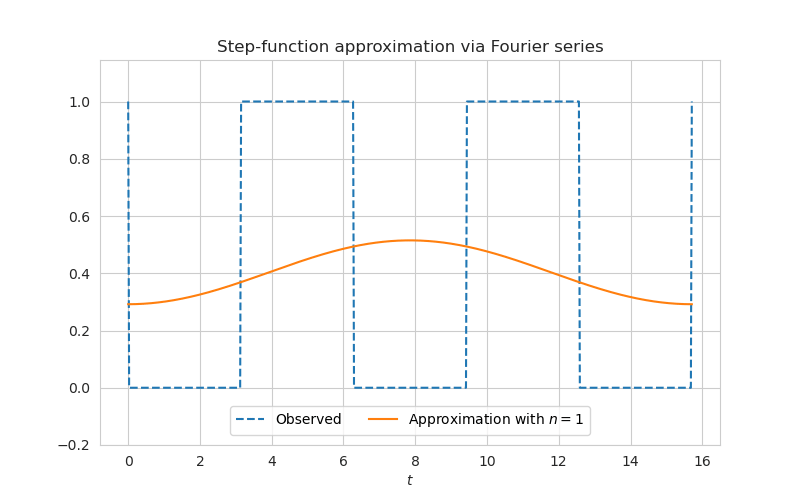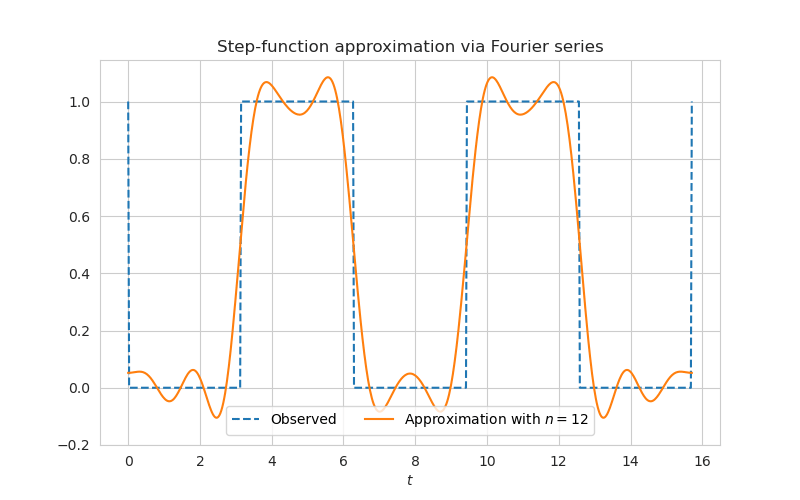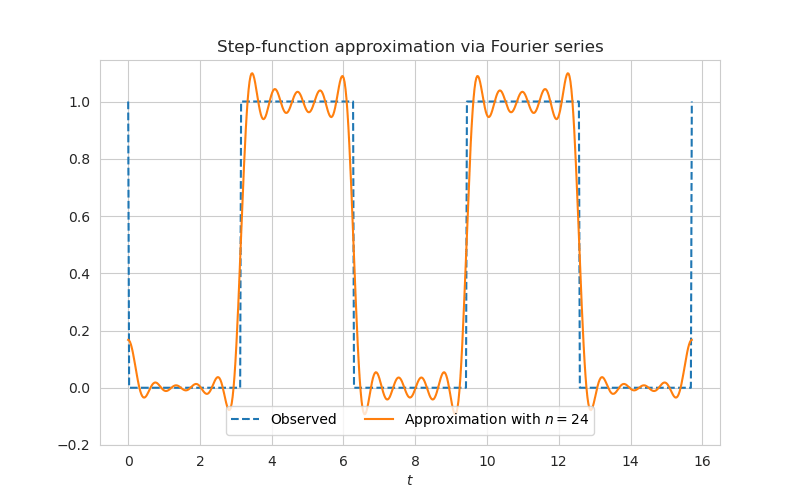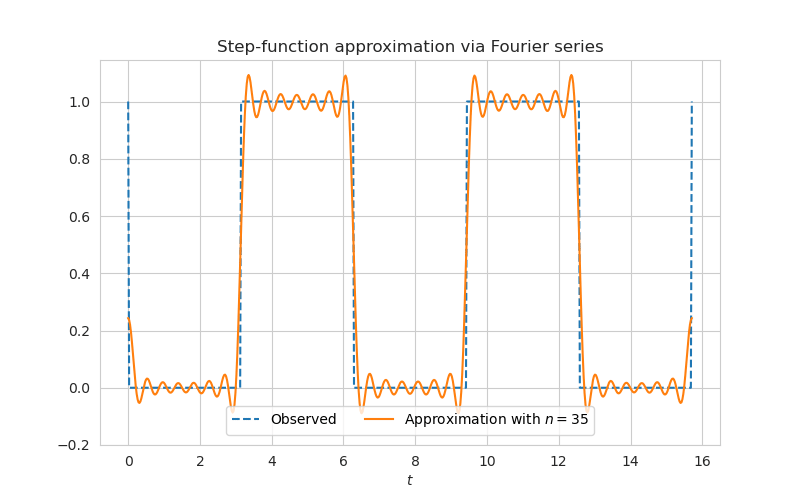
The average value of periodic function $f(t)$ can be calculated via integral using density function, just like the mean of a continuous function:
\[a_0 = \frac{1}{P}\int_{0}^{P} f(t) dt\]Each component $a_n$ and $b_n$ is given as
\(a_n = \frac{2}{P}\int_{0}^{P} f(t) \cos\left(\frac{2 \pi}{P}nt\right) dt\) \(b_n = \frac{2}{P}\int_{0}^{P} f(t) \sin\left(\frac{2 \pi}{P}nt\right) dt\)
The orthogonality property of sine and cosine functions simplifies the computation of coefficients. It ensures that the integral of the product of different harmonics is zero over one period unless the harmonics are the same. Therefore,
\[\int_{0}^{P} \cos(mt) \cos(nt) dt = \begin{cases}0&{\text{if }}m\neq n, \\ \frac{P}{2}&{\text{if }}m=n.\end{cases}\] \[\int_{0}^{P} \sin(mt) \sin(nt) dt = \begin{cases}0&{\text{if }}m\neq n, \\ \frac{P}{2}&{\text{if }}m=n.\end{cases}\] \[\int_{0}^{P} \sin(mt) \cos(nt) dt = 0\]Keeping this in mind we can provide the proof of the formula for either $a_n$ or $b_n$. Let’s do so for $a_n$. First we multiply both parts of the original Fourier series equations by $\cos(mt)$ and integrate them over the period $P$. For simplicity let’s just drop here the scaling factor $2\pi /P$.
\[\int_{0}^{P} f(t)\cos(mt) dt = \int_{0}^{P} \left( a_0 + \sum_{n=1}^{\infty} a_{n} \cos(nt)+\sum_{n=1}^{\infty} b_{n} \sin(nt) \right)\cos(mt) dt\]Integrating over the constant $a_0$ times $\cos(mt)$ will not produce anything because integration over the full period of a periodic function is 0 and scaling it by a constant won’t change anything, so this term becomes 0. Integrating sine times cosine will also produce zero. As for the cosine time cosine, we get zero almost for all cases except when $m=n$.
\[\int_{0}^{P} f(t)\cos(mt) dt = \int_{0}^{P} a_{m} \cos(mt)\cos(mt) dt = a_m \frac{P}{2}\]Dividing this result by $\frac{P}{2}$ produces our formula for $a_n$ which we saw above where instead of $m$ we have the scaled version $2\pi n /P$.
Exponential form of the Fourier series
A more general way to represent the Fourier series is via the sum of rotating vectors through time. This can be achieved by applying the concepts of rotating vectors in the complex space, as was described in this article.
In the existing formula we can replace the sine and cosine terms with their identities in terms of exponential functions.
\[\begin{align*} f(t) &= a_0 + \sum_{n=1}^{\infty} \left[ a_{n} \left( \frac{ e^{i \frac{2 \pi}{P}nt} + e^{-i \frac{2 \pi}{P}nt} }{2} \right) + b_{n} \left( \frac{ e^{i \frac{2 \pi}{P}nt} - e^{-i \frac{2 \pi}{P}nt} }{2i} \right) \right]\\ &= a_0 + \sum_{n=1}^{\infty} \left( \frac{ a_{n} e^{i \frac{2 \pi}{P}nt} + a_{n} e^{-i \frac{2 \pi}{P}nt} }{2} + \frac{ i b_{n} e^{i \frac{2 \pi}{P}nt} - i b_{n} e^{-i \frac{2 \pi}{P}nt} }{2i^{2}} \right)\\ &= a_0 + \sum_{n=1}^{\infty} \left( \frac{ a_{n} e^{i \frac{2 \pi}{P}nt} + a_{n} e^{-i \frac{2 \pi}{P}nt} }{2} - \frac{ i b_{n} e^{i \frac{2 \pi}{P}nt} - i b_{n} e^{-i \frac{2 \pi}{P}nt} }{2} \right)\\ &= a_0 + \frac{1}{2} \sum_{n=1}^{\infty} \left( e^{i \frac{2 \pi}{P}nt} (a_{n} - i b_{n} ) + e^{-i \frac{2 \pi}{P}nt} (a_{n} + i b_{n}) \right)\\ &= a_0 + \sum_{n=1}^{\infty} e^{i \frac{2 \pi}{P}nt} \frac{a_{n} - i b_{n}}{2} + \sum_{n=1}^{\infty} e^{-i \frac{2 \pi}{P}nt} \frac{a_{n} + i b_{n}}{2} \end{align*}\]We can then set the complex number $\frac{a_{n} - i b_{n}}{2}$ as $c_n$, and recognize $\frac{a_{n} + i b_{n}}{2}$ as its conjugate $\overline c_n$.
\[f(t) = a_0 + \sum_{n=1}^{\infty} c_n e^{i \frac{2 \pi}{P}nt} + \sum_{n=1}^{\infty} \overline c_n e^{-i \frac{2 \pi}{P}nt}\]Now let’s take a closer look at $\sum_{n=1}^{\infty} \overline c_n e^{-i \frac{2 \pi}{P}nt}$. With increasing value of $n$ the expression will look like this:
\[\sum_{n=1}^{\infty} \overline c_n e^{-i \frac{2 \pi}{P}nt} = \overline c_1 e^{-i \frac{2 \pi t}{P}} + \overline c_2 e^{-2i \frac{2 \pi t}{P}} + ...\]Notice how increase in $n$ causes decrease in the number before $i$. Considering that the product of two negative numbers is a positive number, the expression could also be rewritten as this:
\[\sum_{n=-1}^{-\infty} c_n e^{i \frac{2 \pi}{P}nt} = c_{-1} e^{-i \frac{2 \pi t}{P}} + c_{-2} e^{-2i \frac{2 \pi t}{P}} + ...\]So the final Fourier series expression in exponential form could be written this concise:
\[f(t) = a_0 + \sum_{n=1}^{\infty} c_n e^{i \frac{2 \pi}{P}nt} + \sum_{n=-1}^{-\infty} c_n e^{i \frac{2 \pi}{P}nt} = \sum_{n=-\infty}^{\infty}c_n e^{i \frac{2 \pi}{P}nt}\]where
\[c_n = \begin{cases}\frac{a_{n} - i b_{n}}{2}&{\text{if }}n > 0, \\ a_0 &{\text{if }}n = 0,\\ \frac{a_{n} + i b_{n}}{2}&{\text{if }}n<0.\end{cases}\]What we eventually get is a sum of vectors in the complex space where each vector rotates at its own rate $n$ through time $t$. If $n$ is positive - the vector rotates counterclockwise, and when negative - the rotation is clockwise. Coefficients $c_n$ represent the magnitudes of the vectors. The sum of vectors could be visually represented by stacking arrows head to tail.
As an elaborate example, see how the Fourier series represented as a sum of rotating vectors (in this case 100 of them) approximate a line drawing:
 The original image is taken from Freepik.
The original image is taken from Freepik.
The integral form of $c_n$ coefficients is calculated by putting in the cosine and sine expressions and then simplifying it using Euler’s formula:
\[c_n = \frac{a_{n} - i b_{n}}{2} = \frac{1}{2} \left[ \frac{2}{P}\int_{0}^{P} f(t) \cos\left(\frac{2 \pi}{P}nt\right) dt - \frac{2}{P}\int_{0}^{P} f(t) \sin\left(\frac{2 \pi}{P}nt\right) dt \right]\] \[c_n = \frac{1}{P}\int_{0}^{P} f(t) e^{-i \frac{2 \pi}{P}nt} dt\]For the negative frequencies we would get the same formula because the product of the negative frequency and a positive imaginary number would result in a negative sign at the exponent.